How do computers store negative numbers? – J005
DeegeU Course
This video “How do computers store negative numbers?” is part of a larger free online class called “Free Java Course Online”. You can find more information about this class on “Free Java Course Online” syllabus.
Try at home
- Try converting a few negative numbers to binary
- Try converting a few negative numbers to hexadecimal
Transcript – How do computers store negative numbers?
In this lesson we’re going to get negative. No, not that kind of negative. I’m more of a “the glass is incorrectly sized” kinda guy. We’re going to talk about negative numbers and how they are stored in Java. If you’re not sure how computers store negative numbers differently, you’ll want to keep watching!
The goals for this lesson are to understand how we store negative numbers in binary. This is also how numbers are stored in Java. We’re going to use something called 2’s complement numbers.
Let’s start with what we know. We talked about binary numbers, and how they are organized to represent positive numbers. Each digit represents a power of two. This is like the normal power of 10 numbers we already use. So how does it work with negative numbers?
Your first thought might be to sacrifice the first digit and use it as a sign bit. Let’s try it. We’ll take a 3 bit number, add -3 and 2. The first number will be 111. That will be our negative 3. Then we’ll add 010. That’s our 2. That gives us 001 or 1. Wait. -3 plus 2… that didn’t work. We should get 101 as a result. Maybe if we add special code for the sign bit? But how do we know when to do that programatically.
The problem with this strategy is it introduces a bunch of cases. A case with 2 positive numbers. A case with 2 negative numbers. A case where the positive number is larger, and a case where the negative number is larger. A case where the positive and negative number add to zero. This really wrecks our simple adder. It won’t work.
Now I’m going to take an aside. We need to talk about something else that might help, and come back to this problem later.
Imagine a clock. On the clock you have numbers from 1 to 12. If it’s 3 o’clock, and you add 12 hours, it’s still 3 o’clock. We’re not looking at days. Just the hour.
If we add three hours, that makes it 6. Add 15 hours, that’s still six. If we subtract 9 hours… yep. Still 6. This works for multiplication too. You can try that one at home.
The reason this works is 3, -9, and 15 are all equivalent numbers for a clock. It doesn’t matter which one you use. You get to the same number in the end. The math way to say it is they are all congruent modulo 12. Don’t worry. That’s not on the quiz. So back to binary land. How can we use this information for our computer numbers?
We do the same thing for our numbers. Imagine our computer holds 3 bits. We’re only using three bits, because I want to show you every possible number. On a computer, the numbers vary from 8 bits to 64 bits. Too many to display here. Now think of the numbers as positions on a clock. We’ll map our numbers this way.
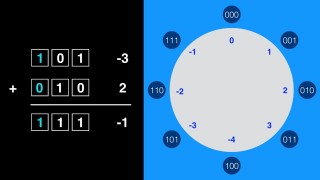
The first bit still means negative, but the other bits are not how we represent positive numbers. For example, -4 is 100 and -1 is 111. So the positive numbers look the same, the negative numbers look weird. What happens now?
Let’s try adding -3 and 2 again. So we add 101 and 010. That gives us 111 which is -1. It works! No special logic. It works because these are equivalent numbers in binary. So how do we calculate this special number when we’re using 16 bits. There really is no magic to it.
To change sign of a number, all the bits are flipped and you add 1. Earlier we had -3. 3 in binary is 011. We flip the bits to get 100. Then we add 1. So the complement number is 101, just like on our clock. If this number were 8 bits, the number would be 11111101. So the number of bits in your mappings matter to calculate the correct equivalent number. Luckily this is all handled behind the scenes for you. However, it is important to understand what the computer is doing.
So this is why we use two’s complement for all numbers in Java. There are no unsigned numbers in Java. Every counting number type is doing this for negative numbers. For some of the larger number types, there are ways to use them unsigned, but we can’t cover that until we get to Number classes. That’s a ways away.
In the next lesson, we’ll actually look at our first type. The byte!
Tools Used
- Java
- NetBeans
Media Credits
All media created and owned by DJ Spiess unless listed below.
- Purzen Clock Face from http://www.openclipart.org
Get the code
The source code for “How do computers store negative numbers?” can be found on Github. If you have Git installed on your system, you can clone the repository by issuing the following command:
git clone https://github.com/deege/deegeu-java-intro.git
Go to the Support > Getting the Code page for more help.
If you find any errors in the code, feel free to let me know or issue a pull request in Git.
Don’t miss another video!
New videos come out every week. Make sure you subscribe!
Comments

DJ Spiess
Your personal instructor
My name is DJ Spiess and I’m a developer with a Masters degree in Computer Science working in Colorado, USA. I primarily work with Java server applications. I started programming as a kid in the 1980s, and I’ve programmed professionally since 1996. My main focus are REST APIs, large-scale data, and mobile development. The last six years I’ve worked on large National Science Foundation projects. You can read more about my development experience on my LinkedIn account.