4 ways to count bits in a byte

Try at home: count bits in a byte

1. Try writing your own methods to count bits in a byte
2. Work through the population count algorithm by hand with different numbers

Transcript – 4 ways to count bits in a byte

Here’s an interesting interview question I recently came across.

Your mission, should you chose to accept, is to count bits. Not just any bits. You have to count all the set bits in a byte. There could be up to 8 of them! So if you laid out the bits in a byte, and counted each time there was a one, how many are
there? Can you do it? If so, how?

Well for starters, one thought might be to use the bitcount function in the Integer class. Easy peasy!

In Java, you can answer this with

return Integer.bitCount(i) == 3;

That’s too easy, and it won’t work. For starters the question specified a byte. The integer bitcount method takes an integer. Pass a byte to it, and it gets cast to an int. Think that doesn’t matter? For example, we know that -1 as a byte is 11111111. So the answer should be 8. Let’s try it.

Create a byte, and set it to minus 1. Print it out, run it, and… the answer is 32. So it’s counting the bits in an integer, not a byte. Since all numbers in Java are 2’s complement numbers, a negative number will give an incorrect answer.

Adding byte to the question makes this question particularly evil for Java developers. Still we learned something from this. There are no built in functions for this, and we need to make sure any operation we use keeps things as a byte.

So the next thought might be to just iterate over the bits, and see what the count is. There’s no iterator on a byte, so we need a different strategy for iteration.

You know the byte has 8 bits. Test the last bit eight times by ANDing it with 1. Keep a counter for when this is not 0. So for the first iteration, we AND the two numbers, and we get 1. Add it to the counter. After each iteration shift the test number by 1. This is
what the code looks like. This always runs 8 times.

That’s because each iteration of the loop tests one bit at a time. 1 byte is 8 bits. So 8 times. We can do better.

Another option is the Kernighan’s bit counting method. That’s the Brian Kernighan from the Kernighan and Ritchie fame from the C language.

This algorithm will loop only for each set bit. So what we do is take our number, and subtract 1 from it. Then AND them. What does that do? That clears the least significant bit. We loop till the test is zero. The number of times we loop is the number of digits. So this improves the count, but it still can loop 8 times if all the bits are set.

We saw earlier that there was a method on Integer to count bits. Wonder if we can use that to figure out a better way to count bits? Let’s try it.

This is a bit mind bending, so I’m going to show the algorithm first with out all the byte casts. The shift and plus operators cause bytes to widen, so you have to make sure you cast back to a byte at every step. That just makes everything messy. And evil. I mentioned evil right?

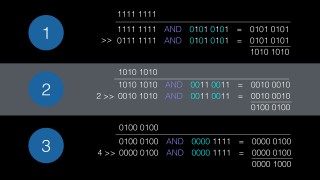
The algorithm is this. Create three masks of bit groups. The first mask has every other bit set, starting with zero. The next one groups bits as two 0s, then two 1s. The last is 4 0s, and 4 1s.

This is sometimes called the Hamming weight or population count.

The cool thing about this algorithm is the number of masks depends on the size of the number we’re testing. The Java code in the Integer class uses 5 masks for 32 bits. 16 uses 4. 8 bits uses 3 masks. See a pattern? Yep, log n. So at worst case, this is going to perform a set of operations log n times. In fact this algorithm has the best worst case performance of any algorithm. Ok… the algorithm.

Let’s try counting -1. That’s 1111 1111 in binary. First AND it with the first mask. Then shift the number by 1, and AND that with the mask. Add the two results together. With that result, we do it again.

This time we use the second mask, and shift by two. Add the results together, and and we have a new result.

Now use the final mask. For this step, we shift by 4. Add the result, and that’s the number of bits in your number. So we get 8 bits in -1 for a byte. Pretty cool huh?

And here’s the code that compiles.

The final way, and probably the quickest, is to create a hashmap for every possible byte. Then just lookup the answer. It’s more memory “intensive” , but we can get away with that. There’s only 256 possible values. Of course you still need to figure out how to populate the hashmap in the first place.

And that is how you count bits! Mission accomplished!